流水算-①

対策レベル
流水算とは川の上りの速さと下りの速さの関係から流速を求めたり、静水時(川の流れがない場合)の速さを求める問題です。
問題は中学校レベルですが、大人になれば純粋に解きづらい問題で不正解の人も多く見受けられる問題です。これまでのSPIの傾向からも出る可能性が大きいので、問題にチャレンジしてみましょう。
早く解くためのヒント
道のり=速さ×時間 の公式は大前提で覚えておくことが必要ですが、それに加えて
- 流速=(下りの速さ-上りの速さ)÷2
- 静水時の速さ=(下りの速さ+上りの速さ)÷2
の公式も必ず覚えておきましょう!
ちなみに、どうして上2つの公式が成り立つかというと、
- 下りの速さ=静水時の(船の)速さ+流速
- 上りの速さ=静水時の(船の)速さ−流速
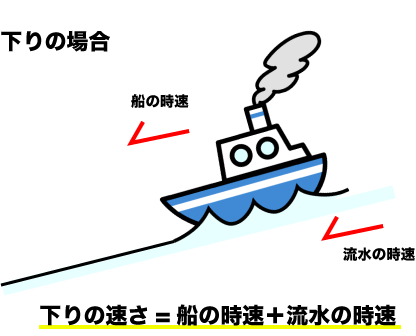

の関係から、連立方程式を解くと導き出すことができます。それでは実際に問題を解いてみましょう。
![]()
そのほかの問題にもチャレンジしてみる
-

-
SPI&一般常識の問題例【数学 (旅人算) 】
旅人算 対策レベル 少し頭を使う必要がある旅人算。答えを導くまでいくつかステップを踏まないといけないので、時間もかかってしまいがち。ただし、出される問題のパターンはどれも似ているので、解答方法をしっ ...
-

-
SPI&一般常識の問題例【数学 (比例) 】
比例 対策レベル SPIや適性検査での比例の問題は比較的単純なものが多く、どれだけ早く解くことができるかがカギです。以下の問題は比例の問題の中でも初球の問題になるので、20秒以内に説くことを目指して ...
-

-
SPI&一般常識の問題例【数学 (濃度-②) 】
濃度算-② 対策レベル 最近は濃度の高いお酒を購入して精製水を混ぜて、自身でアルコール消毒液を作る人も多いのでは?濃度の問題はSPIで頻出する問題です。これを機に、実生活でも役立たせることができる濃 ...
-

-
SPI&一般常識の問題例【数学 (等分) 】
命題 対策レベル 登場する人物が何人もいる計算問題は問題文を理解するまでに時間がかかってしまいます。また、こういった等分の関係性は実際の社会人生活でもよく使われます。SPIは時間が勝負。このように何 ...
-

-
SPI&一般常識の問題例【数学 (組み合わせ) 】
命題 対策レベル 組み合わせの問題は、頭がごちゃごちゃしがちで時間のかかる人も多い問題です。早く回答するために覚えておかなければいけない計算式も存在するので、今一度しっかりと復習をして問題に臨みまし ...
新卒の就活生向けお役立ち記事公開中!
もうすぐ新卒採用のシーズンに突入します。大手サイト以外の就職サービスもフル活用して、理想の企業の内定を勝ち取りましょう!
-

-
新卒の就職活動を有利に進めるにはリクナビ?マイナビ?
2019/6/14
誰よりも良い会社に内定をもらうための就職活動の進め方 当サイトは転職活動をメインにした情報を発信していっていますが、大学3年生・大学院1年生の方はそろそろ就職活動を意識し始める時だと思います。 そこで ...

